Сумма углов треугольника - одна из фундаментальных теорем в геометрии. Рассмотрим основные способы определения этой величины для разных типов треугольников.
Содержание
Сумма углов треугольника - одна из фундаментальных теорем в геометрии. Рассмотрим основные способы определения этой величины для разных типов треугольников.
1. Основная теорема о сумме углов
В любом треугольнике сумма внутренних углов равна 180°. Это утверждение справедливо для всех типов треугольников на плоскости.
2. Методы нахождения суммы углов
| Способ | Применение | Пример |
| Измерение транспортиром | Для нарисованных треугольников | Измерение каждого угла и сложение |
| Использование свойств | Для треугольников с известными параметрами | Вычисление через известные углы |
3. Пошаговый алгоритм вычисления
- Определите тип треугольника (равносторонний, равнобедренный, разносторонний)
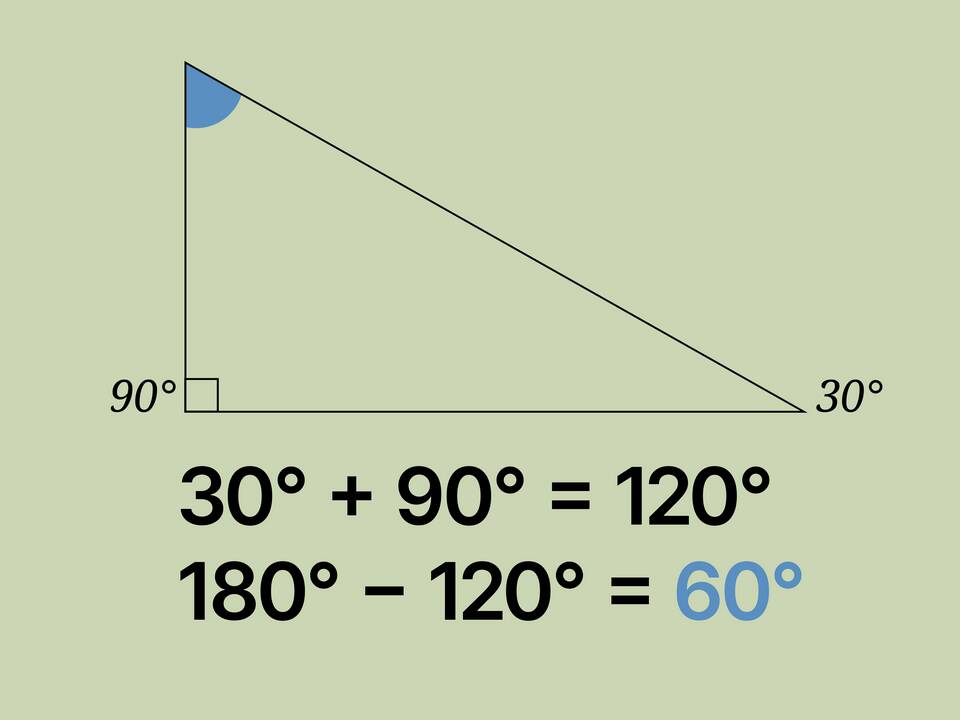
- Если известны два угла, третий найдите по формуле: 180° - (∠A + ∠B)
- Для равностороннего треугольника все углы по 60°
- Для прямоугольного треугольника сумма острых углов 90°
4. Особые случаи
Прямоугольный треугольник:
- Один угол равен 90°
- Сумма двух острых углов составляет 90°
- Формула: ∠A + ∠B = 90°
Равносторонний треугольник:
- Все три угла равны
- Каждый угол составляет 60°
- Сумма: 60° × 3 = 180°
5. Доказательство теоремы
Теорема доказывается через построение параллельной линии к одной из сторон треугольника и использование свойств параллельных прямых и накрест лежащих углов.
Последовательность доказательства:
- Проведите прямую, параллельную одной стороне
- Обозначьте образовавшиеся углы
- Используйте свойства соответственных углов
- Сложите углы в вершине параллельной прямой
6. Практическое применение
- Определение неизвестного угла при известных двух
- Проверка корректности построения треугольников
- Решение задач на построение
- Применение в тригонометрических расчетах
