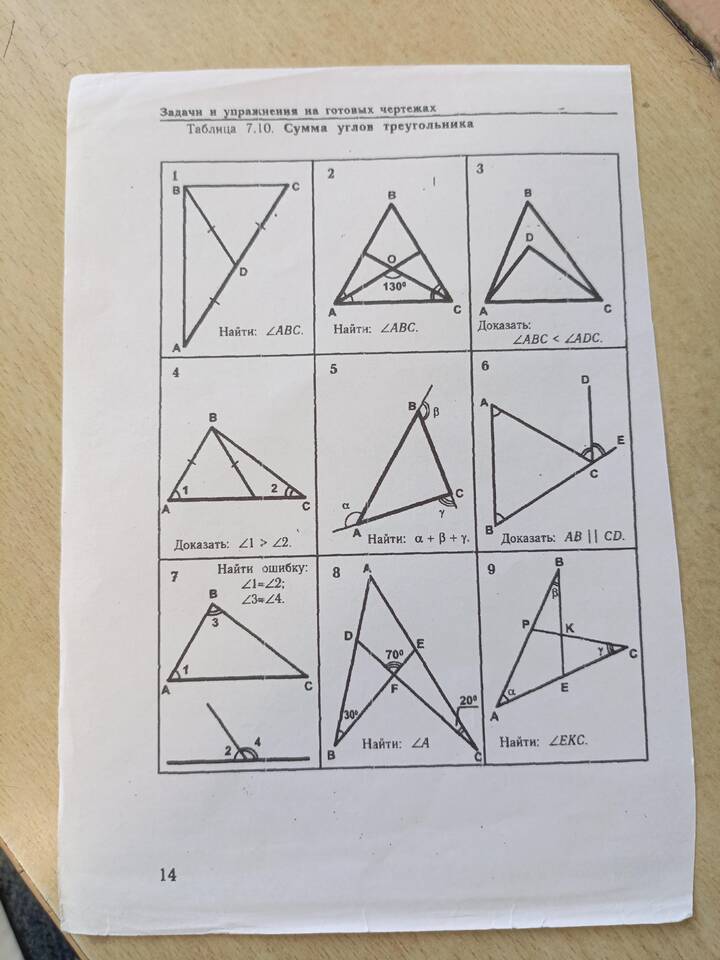
Что такое сумма в геометрии

В геометрии понятие "сумма" имеет несколько специфических значений, отличающихся от арифметического сложения чисел. Оно применяется к различным геометрическим объектам и величинам, помогая решать задачи и доказывать теоремы.

Содержание

Основные виды сумм в геометрии
- Сумма углов многоугольника
Векторные суммы
- Свойства векторных сумм
Геометрические прогрессии и суммы
- Применение сумм в геометрических задачах

Основные виды сумм в геометрии

Тип суммы	Определение	Пример
Сумма углов	Результат сложения величин углов	Сумма углов треугольника равна 180°
Сумма векторов	Вектор, полученный по правилу сложения векторов	Правило параллелограмма или треугольника
Сумма отрезков	Длина, равная сложению длин отрезков	AB + BC = AC, если точка B между A и C

Сумма углов многоугольника

Важное геометрическое свойство:

Треугольник: 180°
Четырехугольник: 360°
n-угольник: (n-2)×180°

Векторные суммы

Сложение векторов производится по особым правилам:

Правило треугольника: конец первого - начало второго
Правило параллелограмма: по диагонали параллелограмма
Правило многоугольника: для нескольких векторов

Свойства векторных сумм

Свойство	Формулировка
Коммутативность	a + b = b + a
Ассоциативность	(a + b) + c = a + (b + c)
Нулевой вектор	a + 0 = a

Координатный метод сложения

Сумма векторов равна сумме соответствующих координат
Пример: (x₁,y₁) + (x₂,y₂) = (x₁+x₂, y₁+y₂)

Геометрические прогрессии и суммы

В геометрии часто встречаются суммы последовательностей:

Сумма бесконечно убывающей прогрессии: S = a₁/(1-q)
Сумма n членов прогрессии: Sₙ = a₁(1-qⁿ)/(1-q)
Применяется в задачах о подобии и площадях

Применение сумм в геометрических задачах

Доказательство равенства фигур
Вычисление длин, площадей и объемов
Решение задач на построение
Анализ геометрических преобразований

Пример практического применения

При расчете пути по векторам перемещения сумма всех векторов дает результирующее перемещение тела из начальной точки в конечную.