Доверительный интервал — это диапазон значений, который с определенной вероятностью содержит истинное значение оцениваемого параметра. Он используется в статистике для оценки точности результатов исследований и измерений.
Содержание
Основные параметры доверительного интервала
| Параметр | Описание |
| Точечная оценка | Выборочное среднее или другая статистика |
| Доверительный уровень | Вероятность (обычно 90%, 95% или 99%) |
| Предельная ошибка | Половина ширины интервала |
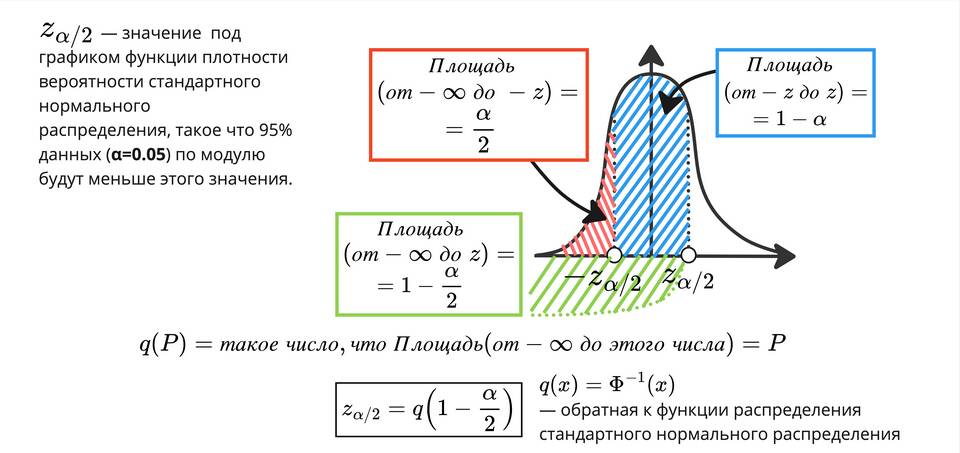
Формула расчета доверительного интервала
- Для среднего при известном σ: x̄ ± z*(σ/√n)
- Для среднего при неизвестном σ: x̄ ± t*(s/√n)
- Для доли: p̂ ± z*√(p̂(1-p̂)/n)
Факторы, влияющие на ширину интервала
- Объем выборки (n) — чем больше выборка, тем уже интервал
- Доверительный уровень — чем выше вероятность, тем шире интервал
- Разброс данных — чем больше вариация, тем шире интервал
Типичные значения доверительных уровней
| Доверительный уровень | Z-значение |
| 90% | 1.645 |
| 95% | 1.960 |
| 99% | 2.576 |
Пример расчета
- Среднее выборки (x̄) = 50
- Стандартное отклонение (σ) = 10
- Объем выборки (n) = 100
- Доверительный уровень 95% (z = 1.96)
- Доверительный интервал: 50 ± 1.96*(10/√100) = [48.04, 51.96]
Доверительный интервал позволяет оценить точность статистических выводов и учитывает случайную изменчивость данных. Его ширина зависит от выбранного уровня доверия, объема выборки и изменчивости данных, что делает его важным инструментом статистического анализа.